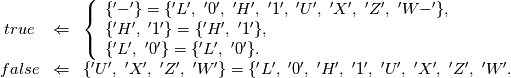Пакет NUMERIC_STD языка VHDL |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
УДК 681.5:004.414.2 ПАКЕТ NUMERIC_STD ЯЗЫКА VHDLН.А. Авдеев, П.Н. Бибило Объединенный институт проблем информатики Национальной академии наук Беларуси, г. Минск
Изучается пакет NUMERIC_STD, предназначенный для согласования арифметических типов данных языка VHDL с логическими типами, построенными на базе девятизначного алфавита моделирования логических схем. Проблема согласования таких типов данных возникает при совместном использовании алгоритмических описаний и структурных описаний логических схем. ВведениеЯзык VHDL (Very high speed integrated circuits Hardware Description Language) широко используется во всем мире для разработки цифровых систем. Первый стандарт VHDL’87 языка появился в 1987 году [1], второй стандарт VHDL’93 – в 1993 году [2]. В 1999 году был принят стандарт VHDL-AMS аналогового надмножества языка VHDL [3], что позволило проводить описание смешанных (цифро-аналоговых) схем. Желательно, чтобы читатель был знаком с основными элементами языка VHDL. С языком VHDL можно познакомиться по книгам [4 – 10]. Для VHDL разработаны и стандартизированы ряд пакетов [6, 7], в которых описаны различные арифметические и логические функции для работы с различными типами данных. Одним из самых важных является пакет STD_LOGIC_1164, в котором декларируется девятизначный тип std_ulogic для описания различных состояний сигналов в проводниках (межсоединениях) между элементами и устройствами и важный подтип std _logic этого типа. Для типа std_logic разрешается назначать значение сигнала из различных источников, что является удобным для описания монтажных соединений в логических схемах и описания шин. Соответствующая “разрешающая” функция имеется в пакете STD_LOGIC_1164. Заметим, что в общем случае ее необходимо написать самому разработчику VHDL-кода. Кроме того, имеющиеся в практике проектирования синтезаторы логических схем (LeonardoSpestrum, XST, Synplify и др.), позволяющие по исходным алгоритмическим VHDL-описаниям синтезировать логические схемы, используют для описания синтезированных схем типы std_logic, std_logic_vector. Последний тип является обобщением типа std_logic на случай векторов – одноразмерных массивов значений типа std_logic. Таким образом, если часть VHDL-проекта синтезирована и описывается в терминах девятизначного логического алфавита, а часть проекта остается на алгоритмическом уровне описания и использует типы INTEGER и NATURAL, то возникает проблема совместимости типов std_logic, std_logic_vector с типами INTEGER и NATURAL. Логические функции, описанные в пакете STD_ LOGIC_1164, не позволяют напрямую использовать тип std_logic совместно с целыми типами INTEGER и NATURAL. Для того чтобы упростить согласование алгоритмических и схемных описаний, разработан VHDL-пакет NUMERIC_STD. Пакет NUMERIC_STD ориентирован на стандарт языка VHDL’93 [2]. Если необходима совместимость с VHDL’87, то требуется из пакета NUMERIC_STD удалить (например, закомментировать двумя знаками дефис) декларации и тела функций xnor (логическая функция “эквивалентость”), sll, srl, rol, ror (функции сдвига). Данная работа посвящена описанию пакета NUMERIC_STD, его возможностям, особенностям и ограничениям, возникающим при моделировании VHDL-программ. Использование данного пакета при синтезе логических схем требует отдельного изучения и в данной работе не рассматривается. Приведенные в статье примеры работы функций пакета были проверены в системе моделирования ModelSim PE 5.7f, в которой содержится рассматриваемая в статье версия пакета NUMERIC_STD. Основные типы данныхВ пакете NUMERIC_STD определены два новых UNSIGNED, SIGNED числовых типа данных и различные арифметические функции над ними, которые поддерживаются системами синтеза. Тип UNSIGNED представляет собой числа без знака в векторном двоичном (булевом) представлении, а тип SIGNED – знаковые числа (числа со знаком). Для векторов SIGNED старший (левый) бит определяет знак числа. Отрицательные числа представляются в дополнительном коде. Например, двоичный вектор “1001” представляет число –7. Вектор “1000” типа UNSIGNED понимается как 8, вектор “1000” типа SIGNED понимается как –8. Базовым элементом типов UNSIGNED и SIGNED является стандартный тип std_logic, описанный в пакете STD_LOGIC_1164. Тип std_logic является многозначным (перечислимым) подтипом типа std_ulogic (табл. 1). Типы UNSIGNED и SIGNED в пакете NUMERIC_STD (далее просто в пакете) определены следующим образом:
Размерности векторов UNSIGNED и SIGNED ограничены типом NATURAL, который определен в пакете STANDARD [7] как подтип типа INTEGER:
В VHDL через S‘high обозначается атрибут “верхняя граница” объекта S. Следовательно, запись INTEGER‘high означает верхнюю границу типа INTEGER. Далее в статье будут использоваться атрибуты ‘left (левая граница), ‘range (диапазон), ‘length (длина диапазона). Заметим также, что в VHDL (и в текстах VHDL-кодов данной статьи) не различаются прописные и строчные буквы.
Таблица 1 – Элементы базового типа std_ulogic
Тип NATURAL включает в себя все положительные целые числа от 0 до 2147483647, а тип INTEGER – положительные и отрицательные числа от -2147483648 до 2147483647. Если перейти к двоичной системе счисления, то тип INTEGER ограничен 32-разрядным вектором, старший (левый) разряд которого означает знак числа (‘0‘ – число положительное, ‘1‘ – число отрицательное). Тип NATURAL ограничен 31-разрядным двоичным вектором. Функции пакета NUMERIC_STDПакет NUMERIC_STD содержит описания следующих функций над типами UNSIGNED и SIGNED:
В основе описания всех функций пакета лежат вспомогательные функции изменения типов (табл. 2), функция преобразования вектора (табл. 3), функции изменения размерности (табл. 4). Функции изменения типовЯзык VHDL позволяет создавать несколько функций с одинаковым именем. Это называется перегрузкой функций. Функция TO_INTEGER (табл. 2) является перегруженной функцией, которая в пакете описана для двух типов аргументов: UNSIGNED и SIGNED. С помощью этой функции можно преобразовать любой вектор SIGNED размерности 1…32 бита или вектор UNSIGNED размерности 1…31 бит в целое число INTEGER или в целое положительное (натуральное) число NATURAL соответственно.
Таблица 2 – Функции изменения типов (Conversion Functions)
Примечание. В табл. 2 (и других таблицах) номер – это номер, который функция имеет (в виде комментария) в пакете NUMERIC_STD. Номер облегчает поиск текста функции в пакете.
Пример применения функции TO_INTEGER.
Не следует использовать векторы, размерность которых превышает размерность типов INTEGER (32 бита) и NATURAL (31 бит), так как в некоторых ситуациях это может привести к неправильному результату функции, который не всегда просто отследить. Функция TO_UNSIGNED позволяет преобразовать положительное целое число NATURAL (из диапазона от 0 до 2147483647) в “беззнаковый” вектор UNSIGNED заданной размерности. Пример применения функции TO_UNSIGNED.
С помощью функции TO_SIGNED можно преобразовать целое число INTEGER (из диапазона от -2147483648 до 2147483647) в знаковый вектор SIGNED заданной размерности. Пример применения функции TO_SIGNED.
Если в функции TO_SIGNED или TO_UNSIGNED задать размерность для результирующего вектора меньше, чем необходимо для представления числа в двоичной форме, то старшие биты вектора-результата отбрасываются (теряются). Например,
Если в результате выполнения операции TO_SIGNED или TO_UNSIGNED потеряны старшие биты, то выдается одно из предупреждений:
при этом работа VHDL-программы не прекращается. Функция TO_01 (табл. 3) побитно преобразует элементы ‘H’, ‘L’ входного вектора (тип SIGNED или UNSIGNED) в ‘1’, ‘0’ соответственно. Если хотя бы один из элементов входного вектора не равен одному из элементов подмножества {‘
Таблица 3 – Функция TO_01 преобразования вектора (Translation Function)
Пример применения функции TO_01.
Функции изменения размерностиФункция RESIZE (табл. 4) изменяет размерность вектора типа SIGNED или UNSIGNED. При увеличении размерности вектора UNSIGNED дополнительные старшие биты результирующего вектора заполняются нулями. При усечении вектора UNSIGNED лишние старшие биты результирующего вектора отбрасываются (теряются). При увеличении вектора SIGNED старший знаковый разряд копируется в дополнительные старшие биты, а при усечении вектора SIGNED
Таблица 4 – Функции изменения размерности (Resize Functions)
Функция RESIZE написана таким образом, что работает со всеми значениями ‘L’, ‘0’, ‘H’, ‘1’, ‘U’, ‘X’, ‘Z’, ‘W’, ‘-‘ старшего (знакового) бита. Примеры, поясняющие работу функции RESIZE, приведены в табл. 5.
Таблица 5 – Примеры работы функции RESIZE
Функцию RESIZE можно реализовать с помощью стандартной операции конкатенации (&). Если необходимо выполнить усечение вектора SIGNED, то выражение
и
эквивалентны. Если необходимо увеличить размерность вектора SIGNED, то выражение
и
эквивалентны. Если необходимо выполнить усечение вектора UNSIGNED, то выражение
и
эквивалентны. Если необходимо увеличить размерность вектора UNSIGNED, то выражение
и
также эквивалентны. Функции RESIZE и TO_01, в отличие от функций TO_INTEGER, TO_UNSIGNED, TO_SIGNED, работают корректно для векторов любой размерности не более 2147483647 бит (размерность типа NATURAL). Экспериментальная проверка была проведена для векторов размерностью 300 бит. Следует обратить внимание на следующее выражение:
В этом выражении аргументом функции TO_INTEGER является переменная (сигнал) a_u типа UNSIGNED, следовательно, в соответствии с табл. 2, функция TO_INTEGER вернет тип NATURAL. Таким образом, переменной d_i типа INTEGER присваивается значение типа NATURAL. Выражение d_i <= TO_INTEGER(a_u); система моделирования ModelSim не считает ошибкой, так как тип NATURAL является подтипом типа INTEGER. Использование такого вызова функции при выполнении VHDL-программы не повлечет ошибки, потому что все значения типа NATURAL входят в множество значений типа INTEGER. Проблемы в работе VHDL-программы могут возникнуть при использовании следующего оператора:
В этом случае переменной c_n типа NATURAL присваивается значение переменной a_s, которая имеет тип SIGNED. Система моделирования также не считает это ошибкой при компиляции VHDL-кода, но при выполнении VHDL-программы не исключен случай, когда переменная a_s примет отрицательное значение, и тогда работа VHDL-программы прекратится, так как отрицательное число нельзя присвоить переменной c_n, которая имеет тип NATURAL. Принимая во внимание вышесказанное, не рекомендуется совместное использование знаковых и “беззнаковых” типов в функциях. Логические операцииВ табл. 6 приведен список логических операций, описанных в пакете NUMERIC_STD.
Таблица 6 – Логические операции (Logical Operators)
Размерности левого (L) и правого (R) аргументов логических функций (табл. 6) обязательно должны совпадать. Размерность результата равна размерности аргументов. Все логические функции выполняются с помощью логических функций, оперирующих с векторами типа std_logic_vector. Данные функции описаны в пакете STD_LOGIC_1164. Пример описания логической функции and в пакете NUMERIC_STD.
При выполнении логических операций значение ‘H‘ эквивалентно ‘1’, а ‘L‘ эквивалентно ‘0’: Пример логической операции and (И).
Если значение компонента вектора равно ‘U’, то и результат любой логической операции над этим компонентом равен ‘U‘. Значение ‘X‘ получается, если компонент вектора равен одному из следующих значений {‘X‘, ‘Z‘, ‘W‘, ‘–’}. Пример логической операции or (ИЛИ).
Операции сдвигаВ пакете описаны две группы операций (операторов) сдвига и вращения (табл. 7). Первая группа состоит из операторов SHIFT_RIGHT (сдвиг вправо), SHIFT_LEFT (сдвиг влево), ROTATE_LEFT (вращение влево), ROTATE_RIGHT (вращение вправо), описанных для векторов типа UNSIGNED и SIGNED: Пример применения операторов сдвига SHIFT_RIGHT, SHIFT_LEFT, ROTATE_RIGHT, ROTATE_LEFT.
Следует обратить внимание на работу оператора SHIFT_RIGHT. Если аргументом этой функции является вектор SIGNED, то в освободившиеся при сдвиге старшие разряды (левые) записывается значение старшего разряда вектора–аргумента.
Таблица 7 – Функции сдвига и вращения (Shift and Rotate Functions)
Пример применения операторов сдвига SHIFT_RIGHT.
Операторы sll (сдвиг влево), srl (сдвиг вправо), rol (вращение влево), ror (вращение вправо) второй группы выполняют те же функции, что и соответствующие операторы из первой группы, но имеют следующие отличия:
Пример применения операторов сдвига sll, srl.
При сдвиге вправо с помощью операторов sll, srl вектора SIGNED не происходит “размножения” знака вектора в освободившиеся старшие разряды результирующего вектора, как в операторе SHIFT_RIGHT Пример применения операторов sll, srl для сдвига вправо вектора SIGNED.
Это связано с особенностью описания тела функций sll, srl в пакете. Пример описания функций сдвига sll, srl в пакете NUMERIC_STD.
Как видно из описания для сдвига вектора вправо, вектор SIGNED преобразуется в вектор UNSIGNED и передается функции SHIFT_RIGHT, которая не размножает старший (знаковый) разряд вектора. Пример применения операторов вращения rol, ror.
Функции сдвига работают с векторами любой длины, которая ограничена размерностью типа NATURAL. Операции сдвига можно заменить стандартным оператором & конкатенации. Пример замены оператора сдвига SHIFT_RIGHT оператором конкатенации.
Пример замены оператора сдвига rol оператором конкатенации
Операции сравненияОписанные в пакете функции сравнения приведены в табл. 8. Если хотя бы один из аргументов L, R (табл. 8) содержит один или несколько символов, не входящих в подмножество {‘H‘,‘L‘,‘0’,‘1’}, то результат сравнения равен false и выдается предупреждение
где * – выполняемая операция сравнения (>, <, <=, >=, =, /=). Сравниваемые с помощью операций табл. 8 векторы могут быть разной длины. Все функции сравнения основаны на функциях сравнения векторов STD_LOGIC_VECTOR из пакета STD_LOGIC_1164.
Таблица 8 – Операции сравнения (Comparison Operators, Match Functions)
Операция STD_MATCH сравнивает два аргумента одинаковых типов на равенство. Аргументы могут быть следующих типов: std_ulogic, unsigned, signed, std_logic_vector, std_ulogic_vector. Типы аргументов обязательно должны совпадать. Операция STD_MATCH сравнивает аргументы по следующим правилам.
Ниже приведена компактная условная запись правил сравнения: Длины аргументов в функции STD_MATCH должны совпадать, в противном случае на экран при моделировании выдается сообщение
и результату присваивается значение false. Возникает ошибка при использовании следующих операторов:
Возможно, система моделирования не может определить, какую функцию использовать, так как не может однозначно идентифицировать тип вектора “101”. Вектор “101” может иметь тип BIT_VECTOR, STD_LOGIC_VECTOR, SIGNED и т.д. Если же тип аргументов задан строго, то ошибки не возникает. Например,
не считается ошибкой. Здесь 10 – число INTEGER. В результате выполнения таких операторов (назначить сигналу c_boolean значение, равное результату проверки отношения равенства двух целых чисел 10) сигнал c_boolean примет значение true.
Арифметические операции (Arithmetic Operators)К арифметическим операциям относятся: abs (абсолютное значение),+ (сложение), – (вычитание), * (умножение), / (деление, т.е. получение целой части частного), rem (получение остатка от деления), mod. Преимуществом типов UNSIGNED и SIGNED над типом STD_LOGIC_VECTOR является то, что для этих типов описаны арифметические операции (1), (2)
не только над векторами типов UNSIGNED, SIGNED, но и операции (3), (4)
над вектором и целым числом. Особенности работы, характерные для всех арифметических функций abs, –, +, *, /, rem, mod, заключаются в следующем:
Функции “–” и “abs” описаны только для типа SIGNED (табл. 9). Данные функции возвращают вектор, размерность которого совпадает с размерностью аргумента. Функция “–” (изменение знака числа) возвращает число, взятое с противоположным знаком, а функция “abs” возвращает абсолютное значение числа (аргумента). Размерность аргументов этих функций ограничена типом NATURAL.
Таблица 9 – Арифметические функции abs, –
Пример применения функций abs, –.
При использовании данных функций необходимо учитывать следующую особенность их выполнения. Например, если взять четырехразрядный вектор SIGNED, присвоить ему значение –8 (“1000”) и применить к нему одну из функций abs, –, то результатом будет являться число –8 (“1000”), а не 8 (“1000”): Пример применения функций abs, –.
Функции сложения, вычитания (табл. 10), умножения (табл. 11), деления (табл. 12) допускают выполнение операции (1), (2) не только над одноименными типами, но и операции (3), (4) для комбинаций типов. Следует придерживаться таких комбинаций и не использовать других, так как в пакете не описаны функции для типов аргументов, отличных от приведенных выше комбинаций. Следующие комбинации типов аргументов арифметических функций “официально” не поддерживаются:
Функция “+” (“–”) осуществляет функцию сложения (разности) двух векторов (которые могут быть разной размерности) или вектора и целого числа. При сложении двух векторов (SIGNED, UNSIGNED) разной размерности результирующий вектор принимает размерность того из аргументов, который имеет большую разрядность.
Таблица 10 – Функции арифметических операций сложения и вычитания
Пример применения функции сложения для векторов различной размерности.
При сложении (вычитании) вектора (SIGNED, UNSIGNED) и целого числа (NATURAL, INTEGER) результирующий вектор (независимо от значения целого числа) имеет размерность вектора. Пример применения функции сложения.
Рассмотрим пример сложения трехразрядного вектора (UNSIGNED) и целого числа 9 (NATURAL):
Очевидно, что для представления r_n в двоичной форме необходимо четыре разряда. Если выполнить операцию сложения:
то результат получается неверным, т.к. целое число 9 (“1001”) преобразуется к вектору размерности 3 и, следовательно, складываются векторы “110” + “001” = “111”. Чтобы избежать такой ошибки, необходимо предварительно перевести целое число в вектор необходимой размерности. Для этого можно использовать функцию to_unsigned:
В данном случае получается правильный результат (15), но если сложить целое число 9 с вектором “111” (7), то заданной выше разрядности недостаточно. Для получения правильного результата необходимо добавить еще один разряд, чтобы не потерять перенос (значение старшего разряда):
или
При умножении двух векторов (табл. 11), размерность результирующего вектора равна сумме размеров векторов-аргументов. Пример применения функции умножения.
Таблица 11 – Функции арифметической операции умножения
При умножении вектора и целого числа, результирующий вектор имеет удвоенную размерность вектора-аргумента: Пример применения функции умножения.
При делении (табл. 12) одного вектора на другой, результатом является вектор, размерность которого равна размерности вектора-делимого.
Таблица 12 – Функции деления
При делении, когда делитель является вектором (UNSIGNED, SIGNED), а делимое целым числом (NATURAL, INTEGER), следует вести контроль того, чтобы значение целого числа-результата не превышало максимально возможного значения вектора-аргумента (делителя) заданной размерности
При возникновении такой ситуации выдается следующее предупреждение об ошибке:
При делении на нуль выдается сообщение об ошибке
но работа VHDL-программы продолжается. При этом результат деления не является определенным. Если значение делителя больше значения делимого, то результат деления 0. Нуль (вектор “00…00” или целое число 0) можно делить на любое число. Результат такой операции всегда 0. Если поделить на –1 наименьшее отрицательное число, представимое вектором заданной разрядности (это число представляется вектором, в котором имеется единица в левом разряде, а остальные разряды содержат нуль), то результатом будет являться само это число:
Эта ошибка подобна ошибке в операции abc. Операторы rem и mod вычисляют остаток от деления. Результирующий вектор для операций rem и mod имеет размерность делителя, если аргументы векторы, а если один из аргументов является целым числом, то размерность результата равна размерности второго аргумента-вектора (табл. 13). В языке VHDL [1] операции rem и mod определяются следующим образом. Для операции L rem R должно выполняться соотношение
где L/R целая часть частного, (L rem R) – результат выполнения операции rem (остаток). Остаток имеет знак операнда L. Для операции L mod R должно выполняться соотношение
где N – некоторое целое число, (L mod R) – результат выполнения операции mod. Результат имеет знак операнда R. Пример выполнения операций rem, mod языка VHDL.
Таблица 13 – Функции rem, mod
Пример применения функций rem, mod (пакета NUMERIC_STD) для типа SIGNED.
Как показано в примерах, для типа SIGNED функции rem, mod пакета NUMERIC_STD корректно реализуют соответствующие операции языка VHDL. Заметим, что результаты операций rem, mod над типом UNSIGNED одинаковы. ЗаключениеПакет NUMERIC_STD является удобным и достаточно надежным средством для согласования типов данных при моделировании смешанных VHDL-описаний – алгоритмических описаний и описаний логических схем. Рекомендуем пользователям, которые начинают использовать данный пакет в своей работе, провести лично проверку найденных (и представленных в данной статье) неточностей в работе функций этого пакета и предусмотреть возможные ошибки. Особенно внимательно нужно следить за размерностями векторов, представляющих результирующие значения операций, так как размерность результата операции числа и вектора определяется именно размерностью вектора. ЛИТЕРАТУРА
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Автор идеи и контента: Бибило П.Н.
Разработчики: Голанов В.А., Зарембо Д.В.
На основе Wordpress CMS
Статистика за сегодня:
Сайт размещен на сервере ОИПИ НАН Беларуси